HQY 一个和谐有爱的空间

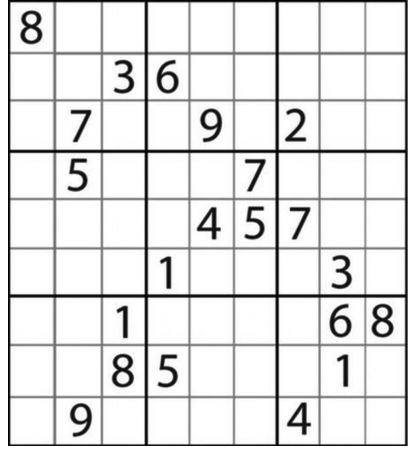
事情大体上是这样的：
“芬兰数学家因卡拉，花费3个月时间设计出了世界上迄今难度最大的数独游戏，而且它只有一个答案。因卡拉说只有思考能力最快、头脑最聪明的人才能破解这个游戏。”这是英国《每日邮报》2012年6月30日的一篇报道。这个号称“世界最难数独”的“超级游戏”，却被扬州一位69岁的农民花三天时间解了出来。而这个具有初中文化的老汉，数独游戏启蒙正是源于扬子晚报。
上面就是题目，简单说下，所谓数独，就是如上图，横向竖向都用1到9填充。然后就是九宫，就是你注意到黑线分成的九个矩阵，也是1到9，下面是这位天才老头用了三天给出的结果。

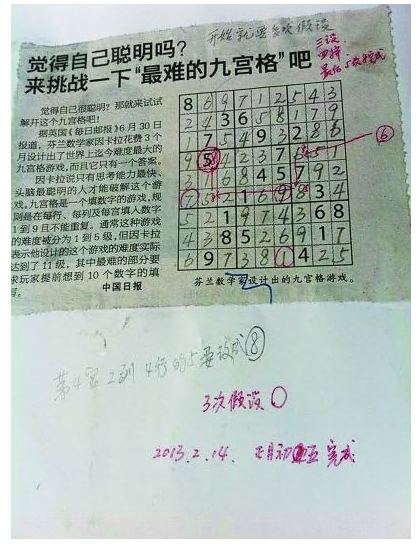
从图片可以看出，天才老头把原题目给改了，然后花了3天算出一个答案，然后自然被封神了，也就是你看的新闻，可见，这就是广大人民眼中的天才。
作为孤独的程序员们，因为计算机与经和大脑密不可分，所以无论是做事还是其它，最终的结果都是人机合体的，所以他们往往能给出世人无法理解的答案和东西。比如:
通过自已的聪明，借助程序去完成。这当然也是本文的大体意思，如果用最粗造的算法，相信很一个会写程序的人都可以写出来，计算结果的时间看CPU能力，以现在的CPU速度，应该都可以很快给出结果。

有兴趣的可以尝试下，人加机器，多久能给出答案!
这里把结果贴一下:

8 1 2 7 5 3 6 4 9
9 4 3 6 8 2 1 7 5
6 7 5 4 9 1 2 8 3
1 5 4 2 3 7 8 9 6
3 6 9 8 4 5 7 2 1
2 8 7 1 6 9 5 3 4
5 2 1 9 7 4 3 6 8
4 3 8 5 2 6 9 1 7
7 9 6 3 1 8 4 5 2

如果以为程序员们仅仅只能做到这一步，那就大错特错了。
下面还有更多的解:
1、Google搜答案，程序员很善于这个，有问题，找Google。
2、使用Google Goggles，这是个图形搜索，只要把图片拍下来一搜，结果都出来了。
3、使用数独计算器软件，当然也可以自已写一个，那么不仅仅是上面这个数堵，理论上所有数独的答案都有了，当然也可以轻松去做一个题。

如果以为程序员们仅仅只能做到这一步，那就大错特错了。

终盘数量

数独中的数字排列千变万化，那么究竟有多少种终盘的数字组合呢？
6,670,903,752,021,072,936,960（约6.67×10的21次方）种组合，2005年由Bertram Felgenhauer和Frazer Jarvis计算出该数字，并将计算方法发布在他们网站上，如果将等价终盘（如旋转、翻转、行行对换，数字对换等变形）不计算，则有5,472,730,538个组合。数独终盘的组合数量都如此惊人，那么数独题目数量就更加不计其数了，因为每个数独终盘又可以制作出无数道合格的数独题目。

如果以为程序员们仅仅只能做到这一步，那还是大错特错了。

标准数独

目前（截止2011年）发现的最少提示数9×9标准数独为17个提示，关于是否有16提示数的合格题目，网络上也争论很久，有发现16提示数双解的，但是仍未发现唯一解。
在2006年Gary McGuire撰写了程序，试图通过暴力法来证明16提示数的数独是否存在，方法很简单，既然Bertram Felgenhauer和Frazer Jarvis已经计算出不等价的终盘总数为5,472,730,538个，那么将每个终盘是16提示的情况都跑一遍，如果没有找到16提示的数独，那么就可以证明最少提示数为17个。
但因为是暴力方法，对于一台单核的电脑来说需要跑30万年才能跑出结果。经过很多人及团队努力，最后Gary McGuire的团队在2009年设计了新的算法，利用Deadly Pattern的思路，花费710万小时CPU时间后，于2012年1月1日提出了9×9标准数独不存在16提示唯一解的证明，继而说明最少需要17个提示数。并将他们的论文以及源代码更新在2006年的页面上。
 由此可见，程序员们借助聪明的脑袋，加上计算机的强大计算机能力，可以完成的事情，已经远远超越普通老百姓，尤其是对电脑理解不是很深的群体的理解范围，所以程序员们不容易被世人所理解也很正常。
你只要稍微借助计算机，就可以完成一般人无法想象的事情.给出他们难于置信的答案，而这种能力已经无法用普通的，不借助计算机所无法理解和承受的范围。

再回顾一下：
芬兰数学家因卡拉，花费3个月时间设计出了世界上迄今难度最大的数独游戏(难度大的依据是什么？)
江苏69岁农民3天破解“世界最难数独”(实际上是改了题目，已经不是原题了)

那么作为一个程序员的你，你可以在这方面，你怎么去出题和去破解呢？你要花多少时间呢？

推荐本站淘宝优惠价购买喜欢的宝贝:

本文链接：https://hqyman.cn/post/8508.html 非本站原创文章欢迎转载，原创文章需保留本站地址！

休息一下~~